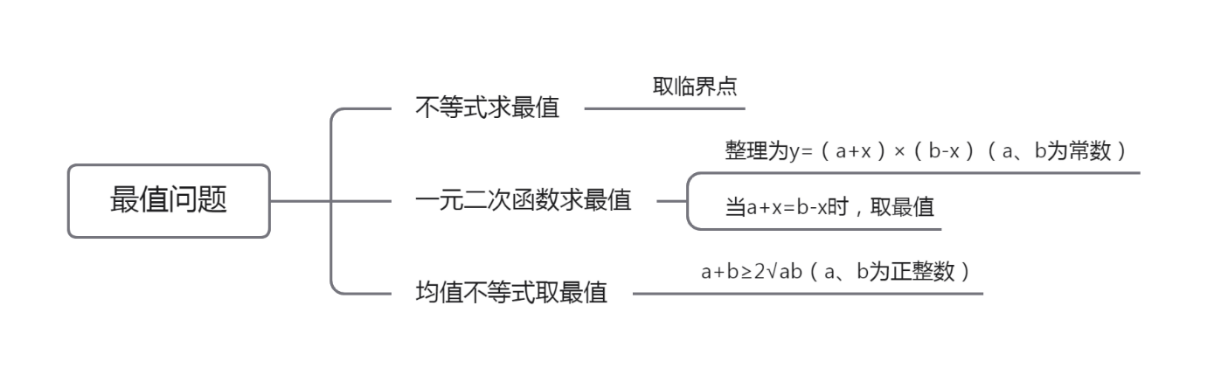
一、基本考情

　　最值问题是数量关系里较常考，且较难的一类题，其难点在于涉及类型多、方法多。为了帮助大家实现考点和真题的有效结合，本文围绕历年国联考真题，分类型介绍下最值问题的解题方法。

　　二、例题解析

　　(一)不等式求最值

　　某文具厂计划每周生产A、B两款文件夹共9000个，其中A款文件夹每个生产成本为1.6元，售价为2.3元，B款文件夹每个生产成本为2元，售价为3元。假设该厂每周在两款文件夹上投入的总生产成本不高于15000元，则要使利润最大，该厂每周应生产A款文件夹()个。

　　A.0B.6000

　　C.7500D.9000

　　设该厂每周生产A款文件夹x个，则生产B款文件夹9000-x个，根据总成本=成本×量，则，整理得，x≥7500，即A款文件夹最少生产7500个。A款文件夹每个的利润为2.3-1.6=0.7(元)，B款文件夹每个的利润为3-2=1(元)，A款单个利润低，B款单个利润高，要使利润最大，则应少生产A款文件夹，多生产B款文件夹。因此，当A款文件夹取临界点7500时，利润最大。

　　因此，选择C选项。

　　(二)一元二次函数求最值

　　某商品的进货单价为80元，销售单价为100元，每天可售出120件，已知销售单价每降低1元，每天可多售出20件。若要实现该商品的销售利润最大化，则销售单价应降低的金额是：

　　A.5元B.6元

　　C.7元D.8元

　　该商品的利润为100-80=20(元)，设销售单价降低了n个1元，即利润降低了n元，则销量多售出20n件。根据总利润=利润×量，总利润=(20-n)(120+20n)=20(20-n)(6+n)。对于形如y=(a+x)×(b-x)的式子，当a+x=b-x时，可取最值。因此，当20-n=6+n，即n=7时，能够实现销售利润最大化。

　　(三)均值不等式求最值

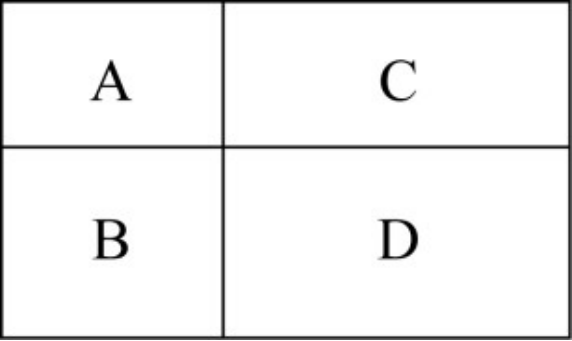
　　村民陶某承包一块长方形种植地，他将地分割成如图所示的4个小长方形，在A、B、C、D四块长方形土地上分别种植西瓜、花生、地瓜、水稻。其中长方形A、B、C的周长分别是20米、24米、28米，那么长方形D的最大面积是：

　　A.42平方米B.49平方米

　　C.64平方米D.81平方米

　　设A的长和宽分别为a、b，由长方形A周长为20米，可得a+b=10①;设B的宽为c，由长方形B周长24米，且长方形B与长方形A的长相同，可得a+c=12②;设C的长为d，由长方形C周长28米，且长方形C与长方形A的宽相同，可得b+d=14③。将①+②+③相加，可得2(a+b)+c+d=36，则c+d=36-2×10=16。根据均值不等式，，则长方形D的面积为c×d≤64。

　　因此，选择C选项。

　　三、技巧点拨

　　由上文可知，最值问题在题目中涉及类型较多。因此，解题时务必先确定类型，再根据题型明确解题方法。